1000桶水,其中一桶有毒,猪喝到毒后会在15分钟内死去,想用1个小时内找到这桶毒水,至少需要几头猪?
先明确一下问题,毒药发作的时间不是精确的,因此你不能每隔0.9秒喂一次猪。
聪明而有经验的老板们应该不难得出应该立即就能得出采取给水桶进行五进制编码以找出身亡的猪喝了哪里的水。这里我在提高了姿势水平之后,描述一下这么做背后的原理是什么。
首先介绍信息熵。这是从物理学中引入的概念,表明 “信息的混乱程度”。 某元素信息熵越高,其信息量越大(如汉字),该元素本身可能出现的状态种类越多。具体计算公式如下:
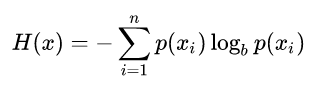
Xi 指代某一个随机事件,p(xi)指这个事件发生的概率, 又名概率质量函数。因其针对描述离散变量而与概率密度函数相对。
b指底数,信息熵没有量纲,因此以计算信息的方式钦定一个量纲。如果b=2,量纲可称作比特bit。一般来说,b等于xi能够出现的所有种类数。
b指底数,信息熵没有量纲,因此以计算信息的方式钦定一个量纲。如果b=2,量纲可称作比特bit。一般来说,b等于xi能够出现的所有种类数。
在这里我们可以认为,猪喝水后15分钟内没有去世,则证明此前饮用的水无毒。以此为前提可以将 一头猪一小时后的情况 分为五种:
- 当场暴毙
- 15~30分钟死了
- 30~45分钟死了
- 45~60分钟死了
- 绝地逢生
因此我们可以取b=5
而由于是随机拿桶给猪灌水,每种状态可以认为是等可能的。
也就是说一只猪一小时后的状态信息的信息熵为
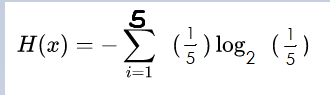
这个值大约是 2.32
请注意这里是一扇猪的信息熵,如果是n条猪,那么b需要变成5的n次方,等价的信息熵也会变。
其实也很简单,答案变成了 2.32n
接下来我们要算1000桶水里1桶有毒这个信息的信息熵,这是因为我们只能用信息量大的事件去推导信息量小的。 学术的说,首先确定最少的猪的数量使得Y状态空间大于X状态空间;其次才能构建Y到X的满射。
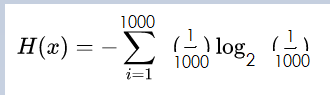
这个值大约是10,准确地说是 9.96
随后我们让猪的信息量大于水的信息量,也就是 n > 9.96 / 2.32 = 4.29,即 n = 5
其实这里我们发现5^5=3125,也就是说3125桶水里1桶有毒也没问题……
至此理论上已经找到了即使在最坏情况下也只需要5坨猪就能给每一桶水编号。工程上怎么实现?这个问题已经不归我管了(装傻
其实要是能理解到这里应该也不难推导出该怎么做
五坨猪
真,我从标题开始就看不懂了