- 稳定:如果a原本在b前面,而a=b,排序之后a仍然在b的前面;
- 不稳定:如果a原本在b的前面,而a=b,排序之后a可能会出现在b的后面;
- 内排序:所有排序操作都在内存中完成;
- 外排序:由于数据太大,因此把数据放在磁盘中,而排序通过磁盘和内存的数据传输才能进行;
- 时间复杂度: 一个算法执行所耗费的时间。
- 空间复杂度:运行完一个程序所需内存的大小。
0.1 不知道从哪搞了一张图,但是暂时只讨论几种内排序。考试要考的各种复杂度,想必会有不少强背的吧。就考前三种还记不住拖出去打死 值得一提的是,矩阵快速转置就是一种外排序
0.2 接下来介绍的可以分成四类,同样是不知道从哪搞的图。
1.选择排序
void selectSort(int arr[], int max)
{
int temp = -1, needsSwap = 0;
for (int i = 0; i < max; i++)
{
temp = i;
needsSwap = 0;
for (int j = i; j < max; j++)
{
if (arr[j] < arr[temp])
{
temp = j;
needsSwap = 1;
}
}
if(needsSwap)
Swap(&arr[i], &arr[temp]);
}
}
2.冒泡排序
这是一个极其简洁的排序思路。它持续地遍历数组,一次比较两个元素,如果它们的顺序错误就把它们交换过来,直到没有元素再需要交换,也就是说该数列已经排序完成。这个算法的名字由来是因为越小的元素会经由交换慢慢“浮”到数列的顶端。
void bubbleSort(int arr[], int max)
{
int issSwap=0;
for(int i=0;i<max;i++)
{
isSwap=0;
for(int j=0;j<max-i-1;j++)
if(arr[j]>arr[j+1])
{
swap(arr[j],arr[j+1]);
isSwap=1;
}
if(isSwap==0)
break;
}
}
3.插入排序
这是一个类似整理扑克牌的排序手段。我们从某一个元素开始,循环选择前面的元素和它比较并且决定插入点,插入前将后续元素移动以腾出空间。因此在顺序表中进行插入排序可能会导致惊人的数据移动量,带来令人不满的时间复杂度。
void insertSort(int arr[], int max)
{
for(int i=0;i<max-1;i++)
{
int current=arr[i+1];
int index=i;
while(index>=0 && arr[index]>current)
{
arr[index+1]=arr[index];
index--;
}
arr[index+1]=current;
}
}
爆破性的while循环导致了大量资源被花费在了移动数组上
4.希尔排序
历史的进程是不可阻挡的,Donald Shell 于1959年改进了插入排序算法,使其成功冲破O(n2)的诅咒。它与插入排序的不同之处在于,它会优先比较距离较远的元素。
希尔排序又叫缩小增量排序,其把记录按下表的一定增量分组,对每组使用直接插入排序算法排序;随着增量逐渐减少,每组包含的关键词越来越多,当增量减至1时,整个文件恰被分成一组,算法便终止。刚才提到的移动数组的爆炸性while循环,此时被巧妙的拆分了。
先给出代码,接着再仔细分析
void shellSort(int arr[], int max)
{
int gap = max;
int i, j, k;
do
{
gap = gap / 3 + 1;
for (i = 0; i < gap; i++)
{
for (j = i + gap; j < max; j += gap)
{
if (arr[j] < arr[j - gap])
{
int temp = arr[j];
for (k = j - gap; k >= 0 && temp < arr[k]; k -= gap)
{
arr[k + gap] = arr[k];
}
arr[k + gap] = temp;
}
}
}
} while (gap > 1);
}
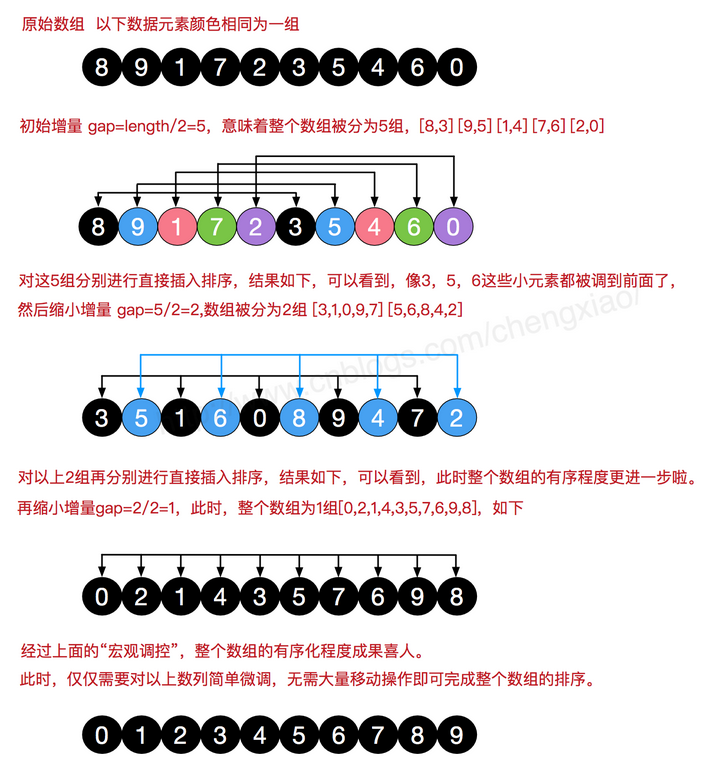
值得一提的是,希尔本人选取的是gap= max/2 但事实上这样会导致出现重复劳动导致效率降低。间隔序列中的数字互质通常被认为很重要:也就是说,除了1之外它们没有公约数。这个约束条件使每一趟排序更有可能保持前一趟排序已排好的效果。希尔最初以N/2为间隔的低效性就是归咎于它没有遵守这个准则。无论选择怎样的分隔,其计算过程都不应该过于复杂而拖累算法本身。不过这种算法的时间复杂度的数学解因为过于困难,还没有被求出来。
5.归并排序
警告:“想要理解递归,首先要理解递归”
归并排序采用分治法(Divide and Conquer),其是一种稳定的排序方法。通过将将已有序的子序列合并,得到完全有序的序列;即先使每个子序列有序,再使子序列段间有序。这种做法会消耗额外的存储空间(临时数组),但能够显著降低时间复杂度。
可以发现有类似二叉树的结构,因此可以用递归实现。当然,也可以转化成迭代的形式。
用递归将数组分割,先分割左半部分再分右半(只是习惯而已),然后每个左右数组一层一层地 排序 并返回。


void merge(int arr[], int left, int mid, int right, int temp[])
{
int l = left, md = mid, mdd = mid + 1, r = right, k = 0, i = 0;
while (l <= md && mdd <= r)
{
if (arr[l] <= arr[mdd])
temp[k++] = arr[l++];
else
temp[k++] = arr[mdd++];
}
while (l <= md)
{
temp[k++] = arr[l++];
}
while (mdd <= r)
{
temp[k++] = arr[mdd++];
}
for (i = 0; i < k; i++)
arr[left + i] = temp[i];
}
void divide(int arr[], int left, int right, int temp[])
{
if (left < right)
{
int mid = (left + right) / 2;
divide(arr, left, mid, temp);
divide(arr, mid + 1, right, temp);
merge(arr, left, mid, right, temp);
}
}
void mergeSort(int arr[], int left, int right,int len)
{
int *temp=(int*)malloc(sizeof(int)*len);
divide(arr, left, right-1, temp);
free(temp);
}
想理解又理解不了很令人恼怒吧(装傻.jpg)?亲可以先去复习一下递归的概念呢(装傻.jpg)
6.快速排序
快速排序是冒泡排序的改进版,也是现有最好的一种内排序,有着最好的时间复杂度。在一些非常非常极端的情况下,它会退化成冒泡排序。它是一种不稳定的排序算法。
说白了,快速排序可以理解成为某一个指定元素寻找插入位置,这个位置的左右两个的元素要么全部大于它,要么全部小于它。随后以两个指针重叠的地方为基准,将数组分开继续调用快速排序,直到区间只有一个元素后返回,就得到了完整的排序。
void QuickSort(int* arr, int l, int r)
{
int left = l;
int right = r;
int key = arr[left];
if (left >= right) //此时排序结束了
{
return;
}
while (left < right)
{
while (left < right && key <= arr[right]) { --right; } if (key > arr[right])
{
arr[left] = arr[right];
++left;
}
while (left < right && key >= arr[left])
{
++left;
}
if (key < arr[left])
{
arr[right] = arr[left];
--right;
}
}
arr[left] = key;
QuickSort(arr, l, left - 1);
QuickSort(arr, left + 1, r);
}
但是,快速排序有一个隐患就是key的选择
比如我们对一个数组{ 9,8,7,6,5 }想通过快速排序来变成从小到大的排序。如果还是选择以第一个元素为枢纽元的话,快速排序就变成选择排序了。
所以,在实际应用中如果数据都是是随机数据,那么选择第几个做key都没有什么不妥。因为这个本来就是看“人品”的。
但是,如果是对于一些比较有规律的数据,我们的“人品”可能就不会太好的。所以常见的有两种选择策略:
一种是使用随机数来做选择。
另一种是取数组中的第一个,最后一个和中间一个,选择数值介于最大和最小之间的。
这一种又叫做“三数中值分割法”。理论上,这两种选择策略还是可能很悲剧的。但概率要小太多了。
7.堆排序
开不开心,惊不惊讶?!我居然写过这个!
其实是文字不好说明白所以才不在这里列的