堆排序是一种利用完全二叉树进行排序的算法，因为数据按大小有序分层，看起来像一个堆垛，被某个闲人命名成堆排序。

介绍就免了，先进行分析：

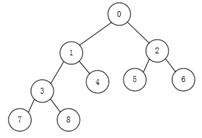
这是个最小堆。对完全二叉树来说父节点和子节点的序号是可以算出来的：

 

标号为n的结点的左孩子为2 * n + 1（如果有），右孩子为2 * n + 2（如果有）。

而标号为n的节点的父节点就是n/2 – 1（这个肯定有）

一般来说完全二叉树可以用数组保存

怎么将给定的一个数组调整成最大/小堆？

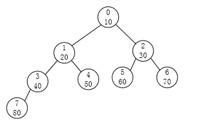
假如想把这个最小堆调整成最大堆，该怎么做？

一般来说一个一个元素比较，最后肯定能成功。

我们就从最下头一个元素开始比较。

首先8/2-1=3，这是最后一个非空子叶节点，比较一下子叶的值

80大于40,40和不存在没法比

交换！

然后是2号 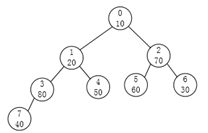和1号

不过这个时候3号节点得重新调整

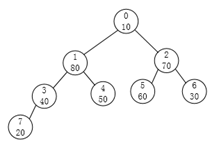
再对0号调整一下

如果把数组展开，可以发现有很多大数字被放到了前面

{80 50 70 40 10 60 30 20}

得到了大根堆之后，我们是可以得到一个最大值了，接下来要做的，就是不断的移除这个堆顶值。将堆顶与堆尾的值进行交换，然后堆的长度减小1，然后进行重新的调整。重复这个过程，直到堆被从顶捡干净。这样每次拎出去的值就是排好序的值了。

 

向下调整运算

void downdown( int heap[], int n, int s ) //n为数组长度，s为待调整的编号
{
   int temp =0 ;
   int i=s;
   while( s*2<=n )
     {
       if( heap[2*s]>heap[i] ) //先讨论左孩子和根的大小
         i=2*s;
       else if( 2*s+1<n && heap[2*s+1]<heap[2*s] ) //再讨论右孩子和根的大小
         i=2*s+1;
       if ( i !=s )  //如果孩子比根小
         {  heap[s]=temp;
            heap[s] = heap[i]
            heap[i]=temp;
            s =i }
        else
           break;  //从这个节点看已经是堆了
          }
}

 

在建立堆的时候，只要对完全二叉树循环调用向下调整运算，即可整理出一个最小/最大堆。

但是在新增元素的时候，需要加在堆底，再逐一比较。因为数组的特性加在堆顶较为浪费资源。

此时需要向上调整

void upup ( int heap[], int n, int s )
{
  int temp;
  if(s==1) return;
  while(s != 1)
   {
     if(heap[s]>heap[s/2])
      {(此处调用函数交换这两个的值);
        s/=2;
      }
     else
       break;
    }
}

虽然偷了个懒但是很好实现的嘛

 

此外，堆排序其实就是优先队列的实现过程。

还有，数据结构中的哨兵元素，可以看下面的文章（请复制手动打开）

https://blog.csdn.net/lison_zhu/article/details/77500811